Data on leaving Certificate Subject Choices Showed That in a Certain year, 24% of Students took Chemistry but not French: Probability Assignment, UCD, Ireland

1. Data on leaving certificate subject choices showed that in a certain year, 24% of students took Chemistry but not French, 51% took French but not Chemistry, and 9% took both French and Chemistry.

Let C be the event that a randomly chosen student took Chemistry, and F be the event the student took French.

(a) Construct an appropriate 2 × 2 table in percentages. Include margin totals.
(b) Compute P(C ∩ F) and
(c) P(C ∪ F) .
(d) Are C and F disjoint (mutually exclusive)? How do you know?
(e) Are C and F independent? How do you know?
(f) For two randomly chosen students, calculate the probability both take French. (Assume students choose courses independently).
(g) For two randomly chosen students, calculate the probability neither takes French.

2. Suppose that A and B are disjoint events for which P(A) = 0.4 and P(B) = 0.2. What is the probability that
(a) either A or B occurs
(b) A occurs but B does not
(c) both A and B occur?

3. 80 percent of drivers have had driver education. During their first year of driving, drivers without driver education have a 0.07 probability of having an accident, but new drivers with driver education have a 0.05 probability of having an accident.

(a) Draw an appropriate tree diagram.

(b) What is the probability a new driver with no accident in the first year had driver education?

4. A classification algorithm classifies 1000 objects in to one of two classes. It incorrectly classifies 13 out of 100 class 1 objects and 53 class 2 objects.
(a) What is the overall error rate?

(b) What proportion of those predicted to belong to class 1 are correctly classified? A competing algorithm run on the same data, classifies 200 objects as class 1, 50% of which are correct. Which algorithm is better?

5. Events A, B and C have probabilities 0.1, 0.2 and 0.1 respectively. Also A and B are mutually exclusive (disjoint), A and C are independent, and B and C are independent. Find the probability that exactly one of the events A,B, and C occur. Hint: draw a Venn diagram.

6. A 2017 survey of Irish undergraduates found that 67.2% of men and 65.1% of women are engaging in a level of drinking that is regarded as unsafe. You can do these calculations in R. (Attach the page with R calculations to your pdf, or hand write in your code and answer.)

(a) Suppose a random sample of 8 male students is collected. Calculate the probability that exactly 6 of the 8 are unsafe drinkers.

(b) What is the probability that exactly 4 of the 8 men are not unsafe drinkers?

(c) What is the probability that 7 or more men are unsafe drinkers?

(d) Repeat calculation (c) for a random sample of 8 women.

(e) What is the expected number of unsafe drinkers among the 16 sampled students?

7. A coffee shop serves an average of 68 customers per hour during the morning. (Attach the page with R calculations to your pdf, or hand write in your code and answer.)

(a) Which of the distributions Binomial, Poisson, Geometric is appropriate for calculating the probability of a given number of customers arriving in an hour?

(b) What are the mean and variance of the number of customers arriving in an hour? What is the standard deviation?

(c) Find the probability the coffee shop serves 70 customers in an hour.

(d) Calculate the probability that 56 customers or less showed up to this coffee shop in an hour?

Extra practice questions

1. Lupus is a medical phenomenon where antibodies that are supposed to attack foreign cells to prevent infections instead see plasma proteins as foreign bodies, leading to a high risk of blood clotting. It is believed that 2% of the population suffer from this disease. The test is 98% accurate if a person
actually has the disease. The test is 74% accurate if a person does not have the disease.

(a) Draw an appropriate tree diagram.

(b) Calculate the probability that someone who tests positive actually has lupus.

(c) There is a line from the television show House that is often used after a patient tests positive for lupus: “It’s never lupus.” What do you think? Is Dr. House correct?

2. In Maynooth University 60% of students travel to campus by public transport. If a random sample of 10 students is selected

(a) Find the probability exactly 6 travel to campus by public transport.

(b) Find the probability more than 6 travel to campus by public transport.

(c) What is the expected number of students in the sample traveling to campus by public transport?

(d) Use R to graph the probability function.

(e) Use R to graph the cumulative probability function.

Extra practice questions- solution

1. Lupus is a medical phenomenon where antibodies that are supposed to attack foreign cells to prevent infections instead see plasma proteins as foreign bodies, leading to a high risk of blood clotting. It is believed that 2% of the population suffer from this disease. The test is 98% accurate if a person
actually has the disease. The test is 74% accurate if a person does not have the disease.

(a) Draw an appropriate tree diagram.

(b) Calculate the probability that someone who tests positive actually has lupus. P(lupus| positive) = P(lupus and positive)/P(positive) = .0196/(.0196+ .2548) = .07

(c) There is a line from the television show House that is often used after a patient tests positive for lupus: “It’s never lupus.” What do you think? Is Dr. House correct?
Dr. House is mostly correct. Someone testing positive is way more likely to be lupus-free than to have the disease.

2. In Maynooth University 60% of students travel to campus by public transport. If a random sample of 10 students is selected

(a) Find the probability exactly 6 travel to campus by public transport.
dbinom(6,10,.6) [1] 0.2508

(b) Find the probability of more than 6 travel to campus by public transport.
1- pbinom(6,10,.6) [1] 0.3823

(c) What is the expected number of students in the sample traveling to campus by public transport?

(d) Use R to graph the probability function.
k <- c(0:10)
plot(k,dbinom(k,size=10,prob=.6),type=”h”,
ylab=”Prob”, main=”Binomial,n=6,p=.6″)

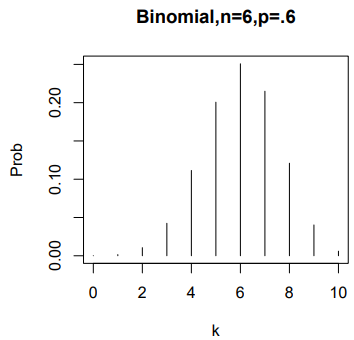
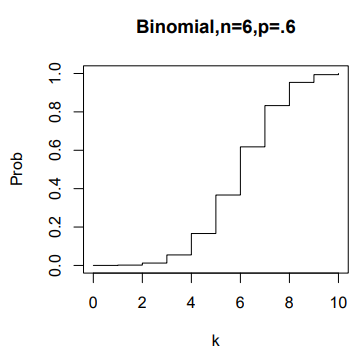
(e) Use R to graph the cumulative probability function.
plot(k,pbinom(k,size=10,prob=.6),type=”s”,
ylab=”Prob”, main=”Binomial,n=6,p=.6″)